LSTM

개요

RNN은 구조가 단순해서 구현하기 쉽지만 치명적인 단점이 있는데 BPTT(Back Propagation Through Time)에서 Gradient Vanishing, 혹은 Gradient Exploding이 일어나기 때문에 시계열 데이터와 같이 시간적으로 멀리 떨어지는 장기 의존 관계를 잘 학습할 수 없다는 것이다.

한마디로 정작 중요한 성능이 좋지 못하다는 것이다.

이를 해결하기 위해서 기존 RNN 구조에 게이트구조가 추가 되는데 대표적으로 LSTM, GRU이 있다.

이번 포스팅에서는 LSTM 에 대한 정리를 한다.

---

소실과 폭발에 대한 대책

Gradient Vanishing, Exploding은 행렬에 곱해지는 동일한 값의 가중치 때문에 일어난다.(Vanishing이냐 Exploding이냐는 입력에 의해 구해지는 행렬이 1에 비해 큰지 크지 않은지에 달려있다.)

이 장기 의존 관계에서의 Vanishing과 Exploding을 해결하는 것이 결국 중요한 과제가 되는데,
그 중 에서 폭발에 대한 전통적인 Gradient Clipping 이라는 기법이 있다.

Gradient Clipping

클리핑의 알고리즘을 의사코드로 표현하면 아래와 같다.

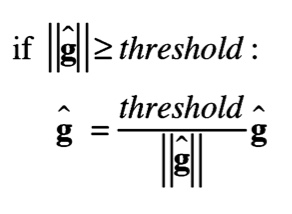
||g^||는 신경망에서 사용되는 모든 매개변수의 기울기를 하나로 모은 것, threshold는 문턱 값을 뜻한다.

의사 코드를 통해서 기울기의 L2 norm이 문턱값 이상이면 그 아래의 수식과 같이 기울기를 수정(문턱 값을 전체 기울기 값(||g^||)으로 나눈 뒤 각 기울기에 곱하는 방식)한다는 의미임을 알 수 있다. 간단한 알고리즘이지만 대체로 잘 작동한다고 한다.

Exploding에 대한 기법은 Clipping으로 해결 가능하다! (대체로는..)

LSTM

하지만 또 하나의 큰 과제인 Vanishing에 대한 대책도 필요하다. 이를 해결하기 위해서는 RNN아키텍쳐를 해부하는 수준까지 가야하는데, 이 때 LSTM 과 GRU 가 등장한다. 물론 LSTM에 대한 포스팅이기 때문에 LSTM에 대해서만 언급한다.

게이트가 추가된 RNN 구조라고 했으니 먼저 RNN 과 LSTM의 도식을 통해 큰 차이를 확인을 할 수 있다.

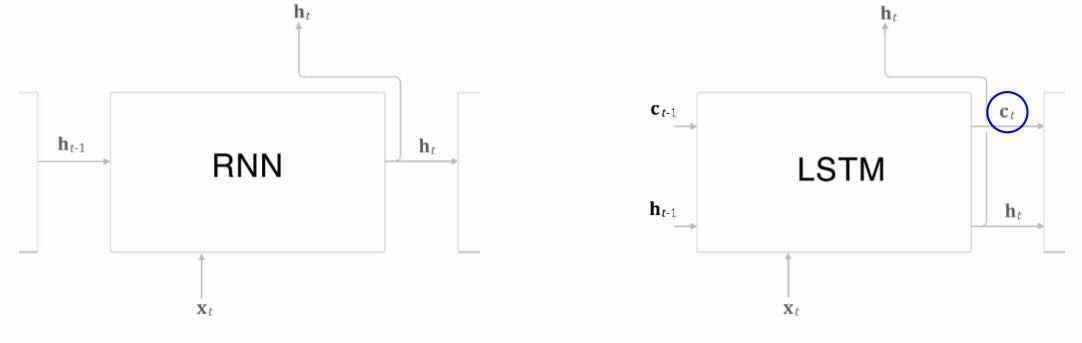
왼쪽 RNN의 도식은 단순화 되었지만

이 안에는 $h_t = tanh(h_{t-1}W_h+x_tW_x+b)$ 의 식이 포함되어 있다.

LSTM은 RNN과 다르게 c라는 경로가 존재하는데 이를 기억 셀( =셀 ) 이라고 하며 이는 LSTM의 기억 메커니즘이다.

셀

기억 셀은 데이터를 LSTM 계층 내에서만 주고 받는다. 해당 LSTM 계층내에서만 데이터가 순환하며 다른 계층으로는 출력되지 않는다.
c는 외부적으로 보이지도 않아서 비유를 좋아하는 내게는 일종의 암흑조직의 뒷거래 같은 느낌이겠구나 하고 생각이 들었다.

하지만 h는 기존 RNN의 메커니즘과 같이 다른 계층으로 출력한다

다시 셀에 대한 이야기로 돌아와서 $c_t$에는 과거 부터에서 어떤 시점 t 까지의 LSTM의 기억이 저장되어 있다.

정리하자면, t 까지의 모든 LSTM의 기억 -> $c_t$ 인 것이다.
이를 토대로 현재 상태의 LSTM에서는 지금 까지의 기억($c_t$)을 바탕으로 은닉 상태 $h_t$를 출력한다.

이는 수식으로 $h_t = tanh(c_t)$로 표현된다.

게이트

output 게이트

지금까지는 게이트가 추가된 RNN 에서 게이트에 사용될 데이터를 만들어줄 데이터를 생성한 것에 지나지 않는다.

그렇다면 정작 게이트는 무엇이고 어떤 역할을 할까?

게이트는 말 그대로 문이다.

문이라면 어떤 것이 드나드는 입구를 통제하는 수단인데, LSTM에서의 게이트의 경우는 데이터, 데이터의 흐름이 될 것이다.

이 문을 얼마나 닫고 열지에 따라 그 흐름 또한 영향을 받게 되는데 이 얼마나 닫고 열지을 열림 상태라고 부른다.

위에서는 게이트에 사용될 데이터를 만들어 주었다고 언급했다. ($tanh(c_t)$)

여기서 게이트는 $tanh(c_t)$의 각 원소(기억 들?)에 대해서 다음 시각에서 출력을 할 때 얼마나 중요할지를 통제 할 것이다.

이는 다음 시각에서 입력으로 받을 출력을 통제하는 게이트 이기 때문에 output 게이트라고 한다. 위의 과정들의 수식은 아래와 같다.

$o = \sigma(x_tW_x^{(o)}+h_{t-1}W_h^{(o)} + b^{(o)})$

과정이 다소 복잡해서 계산 그래프를 통해서 개략적이나마 이해할 수 있었다.

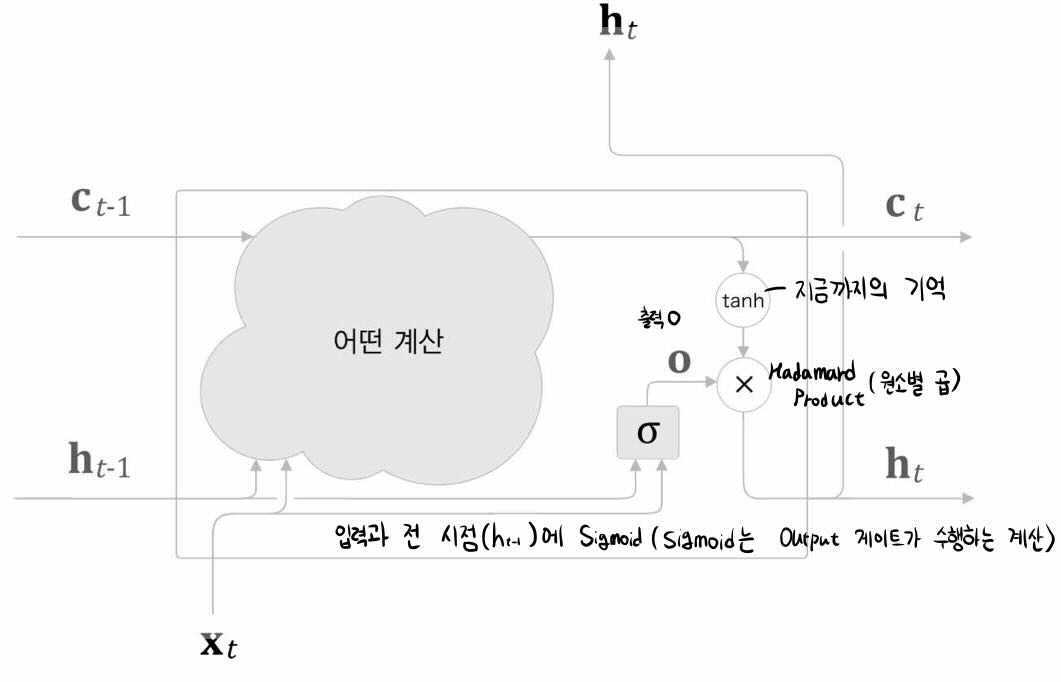
$\sigma$ 의 출력은 0.0과 1.0사이의 실수이며 이는 위에서 언급했던 열림 상태 를 뜻한다.

forget 게이트

어떤 것을 학습(기계 학습 뿐 아니라!)할 때는 기억도 중요하지만 그 내용의 중요도에 따라 필요없다고 판단되는 경우에 잊어버리는 것이 더 중요한 내용을 명료하게 기억하게 끔 도와준다.

LSTM에서는 이런 일을 해주는 것이 forget gate다.

forget 게이트가 수행하는 계산은 아래의 계산식과 같다.

$f = \sigma(x_tW_x^{(f)}+h_{t-1}W_h^{(t)}+b^{(f)})$

output 게이트의 식을 접하고나니 그래도 더 쉽게 다가왔다.

먼저 전 시점과 전 상태, 편향을 모두 더한 값에 $\sigma$ 를 취해주고 그 전 기억정보($c_{t-1}$)에 원소별 곱을 통해서 기억정보에 어떤 기억들을 남기고 통과시킬지 통제한다.

아주 단순화해서 output 게이트는 상태 값을 갱신 시키는 거라면 forget 게이트는 기억 값을 갱신 시킨다고 생각되었다.

gate 게이트(?)

forget 게이트에서는 얼마나 잊을지를 정해줬다. 얼마나 잊을지만 정해주고 나머지는 알아서 기억해준다면 좋겠지만, 안타깝게도 그렇지 못한가보다.

그래서 cs231n에서는 gate gate라고 칭해준(엄밀하게 게이트가 아니라고 한다.)
기억해야 할 정보를 추가해주는 작업을 해야한다.

얼마나 제어할지가 아니라 얼마나 추가할지 정해주어야 하기 때문에 이 곳에서는 활성화 함수를 $\sigma()$가 아닌 $tanh()$를 사용해준다.

이러한 내용을 수식으로 표현하면 다음과 같다.

$g = tanh(x_tW_x^{(g)} + h_{t-1}W_h^{(g)}+b^{(g)})$

input gate

마지막으로 위에서 gate 게이트라고 칭했던 g에 게이트를 추가한다.

input 게이트에서는 g의 원소의 가치가 정보로써 얼마나 가치가 큰지 판단한다.

한마디로 새로운 정보 또한 통제 하는 것이다.

이는 사람이 무비판적인 태도로 정보를 받아들일 때 쓸모없는 정보가 많이 개입되는 것을 방지하는 과정과 비슷하다는 생각이 들었다.
(영국에 있는 연구소에서 나온 정보라던지)

이 게이트에서 수행되는 계산식은 아래와 같다.

$i = \sigma(x_tW_x^{(i)}+h_{t-1}W_h^{(i)} + b^{(i)})$

위에서 설명했던 것과 같이 정보를 통제 해야 하기 때문에 활성화 함수는 $\sigma$가 사용됐다.

이렇게 나온 i는 g(gate 게이트에서의 결과, 즉 새로운 정보)와 원소별 곱을 수행한 뒤 f(forget 게이트의 결과)에 더해져서 최종 기억 셀($c_t$)을 만들어 낸다.

위에서 나왔던 모든 과정의 계산 그래프는 아래와 같다.

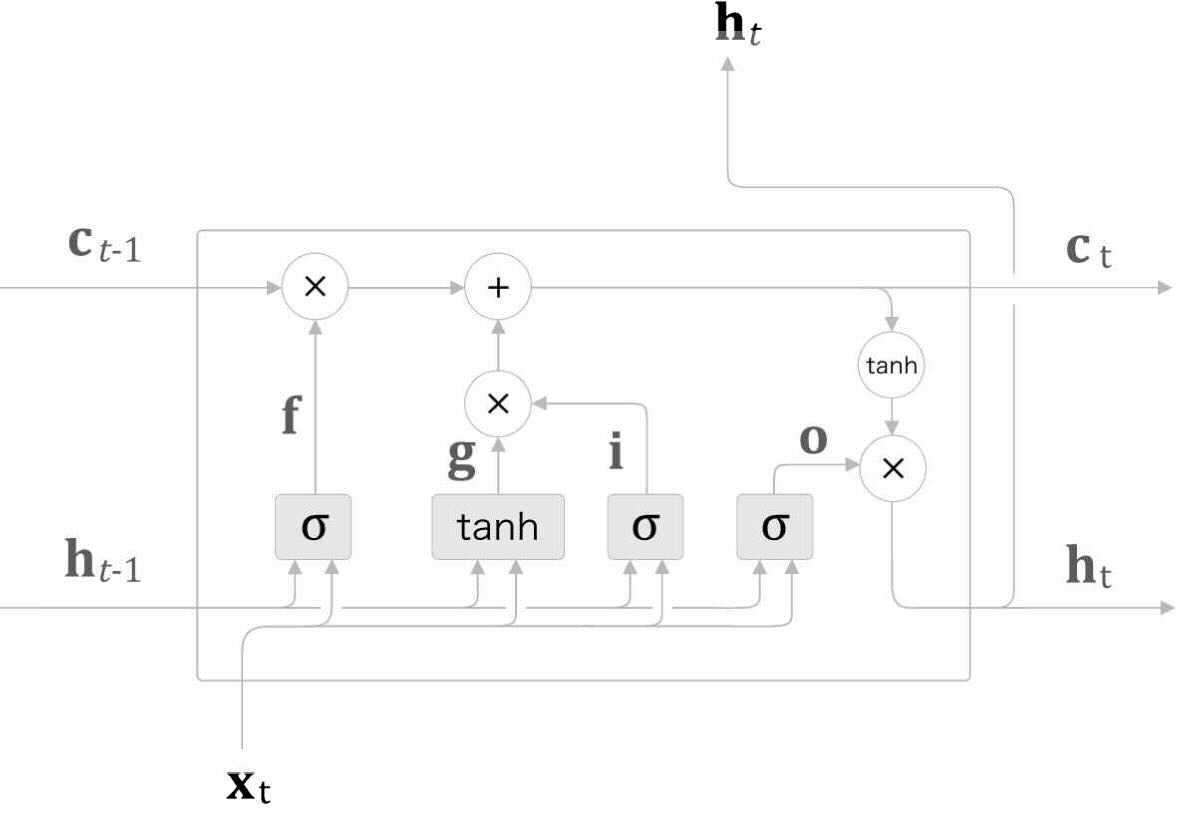
이상 게이트가 추가된 RNN, LSTM에 대한 포스팅을 마친다.

ref.

[사이토 코키(2019), 밑바닥 부터 시작하는 딥러닝2(한빛 미디어)]

https://excelsior-cjh.tistory.com/89