Data preprocessing(데이터 전처리) Normalization

개요

사람은 집을 살 때 방의 수, 위치, 연식 등을 통해서 가격을 고려하고 구매할 것인지 결정한다. 이 때 가격을 고려하는 과정을 딥러닝 모델에게 맡긴다면 사람과 비슷한 가격을 측정(고려)할까?

데이터를 날 것 그대로 넣어준다면 전혀 다른 예측을 보여줄 것이다. 이는 단위에 대한 가치를 인지하는 사람과는 다르게 모델이 보기에는 큰 수, 작은 수일 뿐이기 때문이다.
가령, 방의 개수가 하나이고 그 건물이 지어진 연도가 2001년도인 집과 같은 해에 지어진 건물의 방이 10개인 집이 있다고 한다면 모델은 집의 가격을 고려하는데에 방의 개수보다는 훨씬 큰 수인 2001이라는 수(연식)에 더욱 중점을 두고 학습을 하게 된다.

좀 더 간결하게 말하자면, 모델이 학습하는데 중요하게 여기는 것은 그 데이터의 스케일이기 때문에 방의 개수 정도는 그다지 고려하지 않는 것이다.

따라서 우리가 원하는 예측을 하기 위해서는 스케일이 큰 한 요소만 고려하는 것이 아니라 다른 요소들도 같이 고려할 수 있도록 데이터를 정제해줘야 한다. 이것이 Normalization(정규화)이다.

Normalizations

정규화는 정말 다양하다.

Min-Max Normalization

Z-score Normalization

Batch Normalization

Layer Normalization

Group Normalization

Weight Normalization

Weight Standardization

…

이 중에서 널리 사용되는 Min-Max, Z-Score Normalization에 대해서 정리했다.

각각의 장단점이 있기 때문에 잘 이해하고 있어야 원하는 경우에 원하는 정규화를 사용할 수 있다.

1. Min-Max Normaliztation

가장 흔한 정규화로 모든 feature에 대해서 0과 1사이의 값으로 변화시킨다. Min-Max 정규화 공식은 아래와 같다.

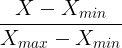
Min-Max 정규화는 큰 단점이 있는데, 이상치에 취약하다는 것이다.
아래는 100개의 값 중 99개는 0과 40사이에 있고, 1개의 값이 100인 경우를 Min-Max 정규화를 거친 모습이다.

<img alt = "min_max_png.png"src = "../../assets/images/DataPreprocessing/Normalization/min_max_png.png " width = "50%">

y축에 관해서는 정규화가 되었지만 x축에 관해서는 별다른 효과를 보지 못한 모습이다.

이를 해결하기 위해서 Z-score Normalization을 사용한다.

2. Z-Score Normalization

Z-Score 정규화는 Min-Max의 단점인 이상치를 고려한 정규화이다. 정규화 공식은 아래와 같다.

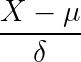
δ는 표준편차, γ는 평균을 뜻한다.
feature의 값이 평균보다 큰가 작은가에 따라 그 수가 음수인가, 양수인가가 정해지며 표준편차로 그 크기가 정해진다.
이 z-score는 그 값이 클수록 값이 넓게 퍼져있는 것이고, 정규화되는 값이 0에 가깝다고 할 수 있다.

이는 Standardization으로도 부르는데, 둘의 이름을 갖는 것은 위의 공식이 z-score를 구하는 공식이기 때문이다.
이렇게 Z-Score를 얻어내고, 평균에서 크게 벗어난 outlier일수록 큰 절대값을 가지고 이 score가 -2에서 2를 벗어난 값들 즉 이상치들을 제외하는 것이다. 또한 -2에서 2사이의 값을 갖기 때문에 0을 중앙값으로 갖는 값을 가질 수 있다.

그래서?

Normalization은 어떤 데이터의 Scale을 줄여준다.
scale을 줄여줌으로써 학습 어떤 데이터에서 한 feature가 다른 feature에 비해 지나치게 큰 값 들을 가진다면 Normalization해주는 것이 적절할 것이다.

Z-Score Normalization(Standaridization)은 outlier(군집에서 벗어난 값)을 제거한다. scale이 줄여지긴 하지만 정해준 기준, 모두 동일한 척도로 정규화된 데이터를 생성하지 않는다.