프로그래머스[ LV2 | Python ] k진수에서 소수 개수 구하기

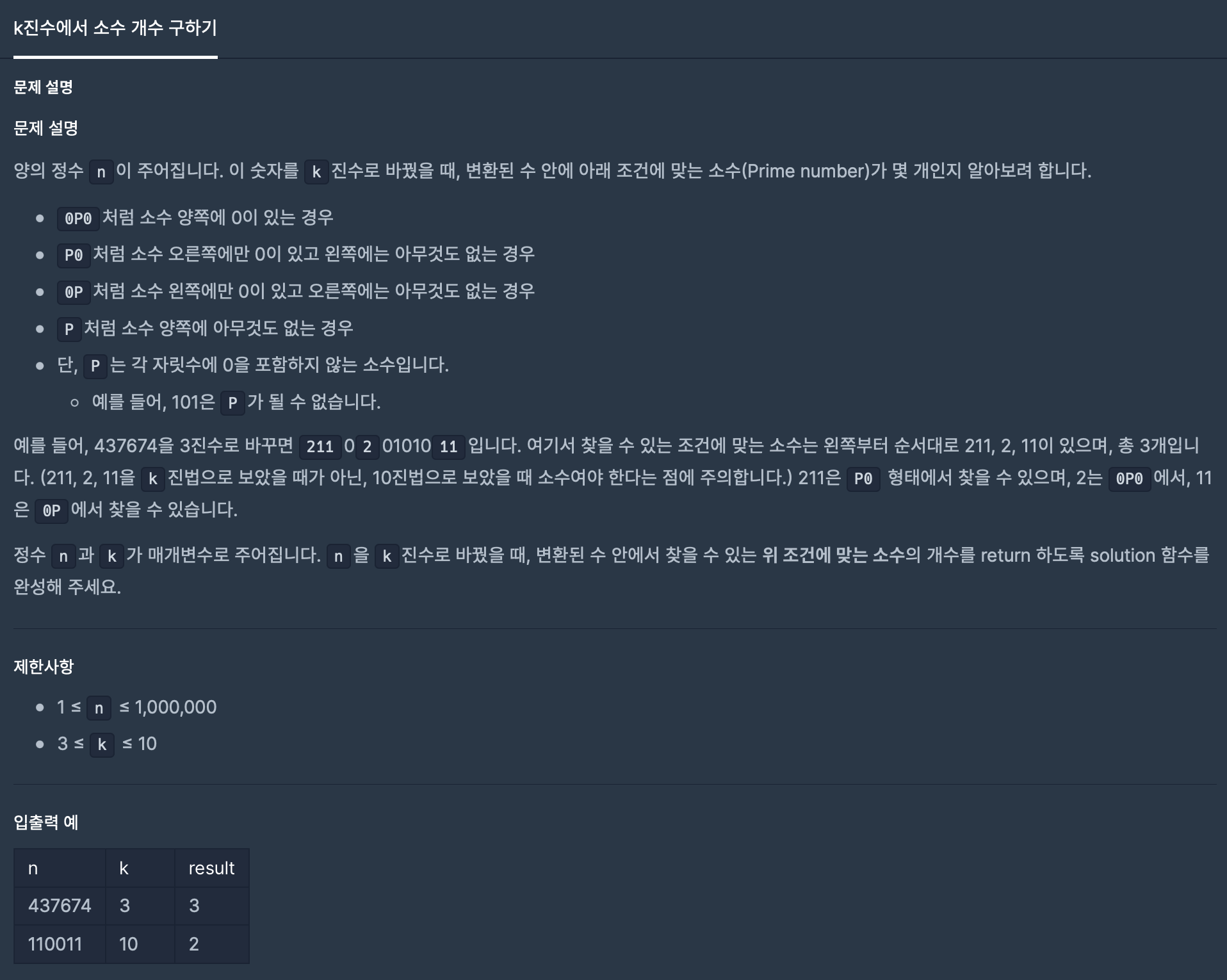
문제

https://programmers.co.kr/learn/courses/30/lessons/92335

풀이

주어진 n을 k진수화 한 결과 값을 주어진 조건에 맞게 0을 기준으로 k진수값을 잘라준다.

잘라준 값을 소수인지 판별하여 결과를 출력한다.

import math
def solution(n, k):
    answer = 0

    def is_prime(x):
        if x == 1:
            return False
        for i in range(2, int(math.sqrt(x)) + 1):
            if x % i == 0:
                return False
        return True
                
    def to_n(n, k):
        tmp = ''
        while n > 0:
            n, mod = divmod(n, k)
            tmp += str(mod)
        return tmp[::-1] 
    
    target = to_n(n,k).split('0')
    
    for t in target:
        if t!='' and is_prime(int(t)):
            answer+=1
    return answer

생각 & 정리

문제 설명에서 잘라진 값 211,2,11을 k진법이 아닌 10진법으로 보았을 때 소수여야한다는 조건을 착오해 완전히 반대로 생각했다.

오해한 부분을 다시생각하여 다시 해결하는데, 1번 케이스와 11번 케이스에서 시간 초과가 났는데, 기본적인 소수판별 알고리즘은 많은 시간이 필요할 것으로 생각해서 에라토스테네스의 체를 이용한 소수 판별을 사용했는데, 원하는 값 이하의 모든 소수를 찾는 알고리즘이었기 때문에 적절치 못했던 것 같다.

따라서 루트를 이용하는 소수판별을 이용하여 해결했다.
이 때 실제로 세 소수판별법의 성능이 얼마나 차이나는지 문뜩 궁금해져 이곳에서 실험해보았다.