백준[ 3020 | Python ] 개똥벌레

문제

https://www.acmicpc.net/problem/3020

풀이

누적합과 이분탐색을 이용해 해결할 수 있는 문제다.
먼저 종유석과 석순을 나누어 배열에 저장하고 정렬한다. 예제 1에서 이 과정을 거치면 아래와 같아진다.

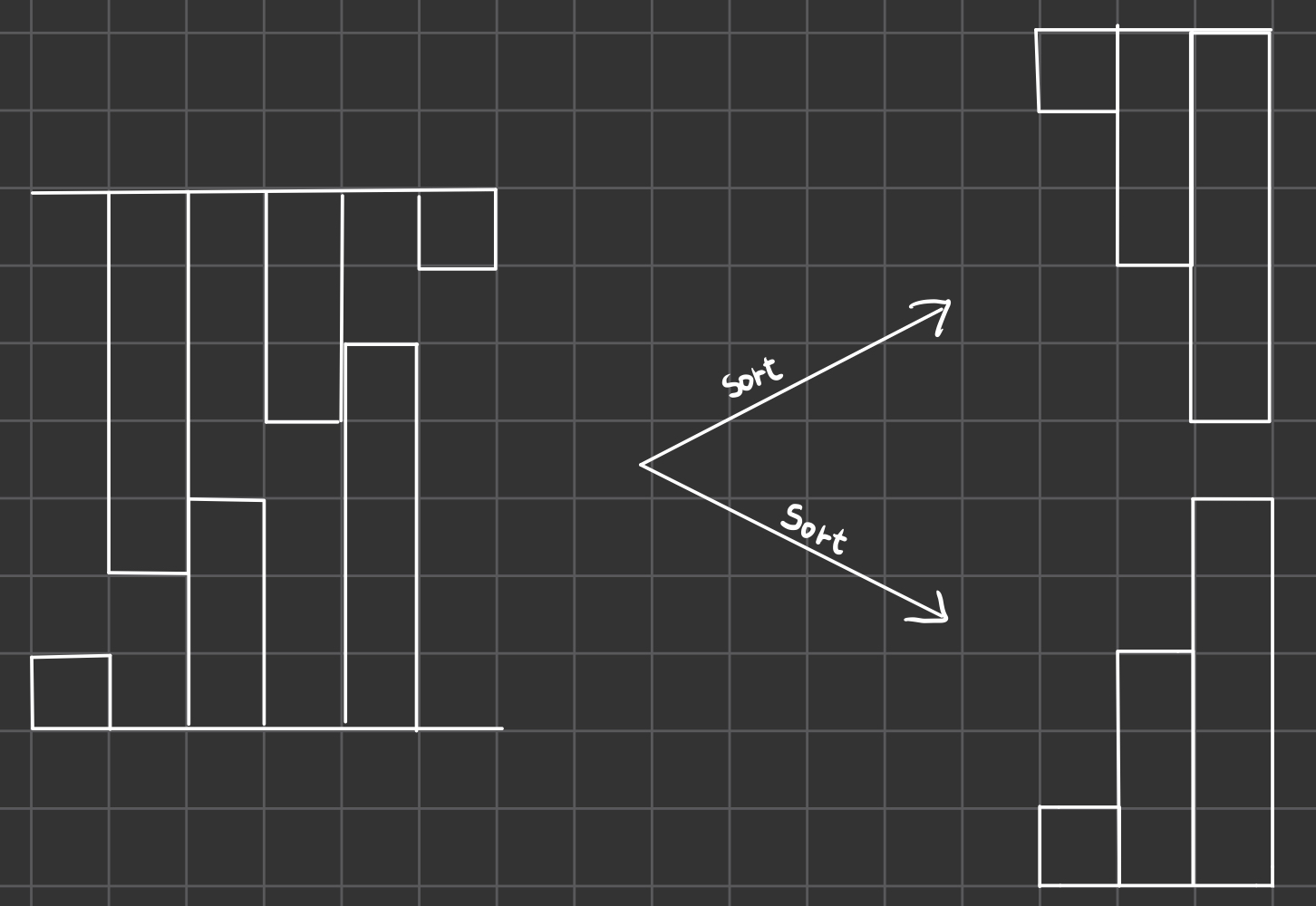
이렇게 나누어진 종유석과 석순을 현재 탐색하는 높이에서 이분탐색을 진행한다.
여기서 종유석을 탐색하는 경우, 위치를 고려하여 최대높이에서 현재 탐색 높이를 빼주어 탐색해주어야한다.

bisect_left는 원하는 값의 인덱스를 return 한다. 정확히는 target값이 list에 삽입될 위치를 return하는 것인데 bisect_left([1,2,3],4)의 경우에는 return값은 3이 된다.

이를 활용하면 이분 탐색으로 정렬된 리스트에서의 현재 높이 값에 포함되지 않는 석순과 종유석의 개수를 구할 수 있게 된다.

위의 과정을 주어진 값 H만큼 탐색하며 최소값을 갱신하여 해결한다.

import sys
from bisect import bisect_left
input = sys.stdin.readline

N,H = map(int,input().split())
cave = [int(input().rstrip()) for _ in range (N)]

top, bot = [],[]
for i in range(N):
    if i%2 == 0:
        bot.append(cave[i])
    else:
        top.append(cave[i])

top.sort()
bot.sort()
cnt = 1

min_val = float('inf')
for h in range(1,H+1):
    t, b = bisect_left(top, (H+1)-h),bisect_left(bot, h)
    #정렬된 종유석과 석순에서 h높이를 가진 것들의 인덱스를 추출해 개수를 알아낼 수 있다.
    total = N - (t+b)
    if total < min_val:
        min_val = total
        cnt = 1
    elif total == min_val:
        cnt += 1

print(min_val, cnt)

생각 & 정리

bisect_left를 이전까지는 그 값의 인덱스 자체를 반환하는 것으로 착각하고 있었는데 참고 블로그에서 올려준 docs 덕분에 생각을 바로잡을 수 있었다.
또 이분탐색을 진행하기 위해서는 배열이 정렬되어있어야 된다는 점을 이용할 수 있음을 다시금 깨닫게 되는 계기가 되었다.

참고

https://cotak.tistory.com/152