백준[ 1660 | Python ] 캡틴 이다솜

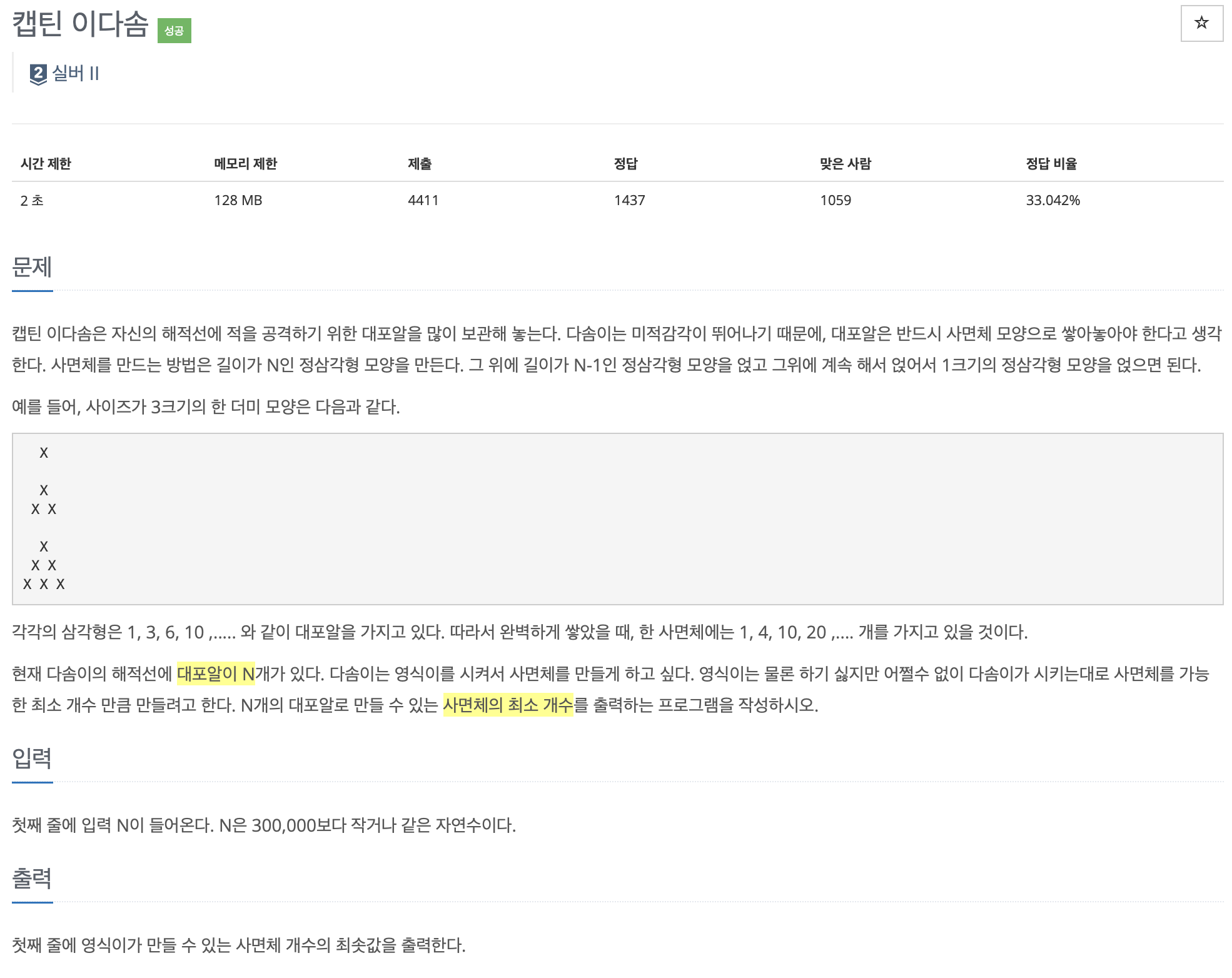
문제

https://www.acmicpc.net/problem/1660

풀이

먼저 각 층 마다 쓰이는 대포알의 개수를 점화식을 통해서 알아낸다.
이후 dp를 통해서 사면체의 최소 개수를 내야 하므로 dp테이블은 높은 값으로 초기화 해 준 뒤에
dp테이블을 탐색함과 동시에 이전에 구했던 각 층 별 대포알의 개수를 함께 탐색해준다.

이 때 n으로 주어진 대포알 개수보다 탐색하고 있는 사면체의 대포알 개수가 더 크다면
반복문을 탈출하고 또, 탐색하고 있는 대포알 개수가 n과 같다면 필요한 사면체는 1개이기 때문에 dp테이블에 1을 저장하고 탈출한다.

위 두 경우가 아니라면 dp테이블을 갱신해 주어야하는데, 이미 저장된 i개의 대포알을 사용한 사면체의 개수와 dp[i-b], 즉 i개의 대포알에서 b개의 대포알을 뺌으로서 생긴 사면체를 한 개 더해준 사면체의 개수를 비교해 둘 중 더 작은 사면체의 개수를 dp테이블에 저장한다.

import sys
input = sys.stdin.readline

n = int(input().rstrip())
balls = []
b = 0
i = 1
while b < n:
    b += (i*(i+1))//2 #점화식
    balls.append(b)#임의의 수 n 층일 때 포탄의 수
    i+=1
MAX = sys.maxsize
dp = [MAX]*(n+1)
for i in range(1, n+1):
    for b in balls:
        if b >= i:
            if b == i:
                dp[i] = 1
            break
        dp[i] = min(dp[i],1 + dp[i-b])#포탄이 n개 일 때 b만큼의 포탄을 가진 사면체 + 1
print(dp[n])

생각 & 정리

점화식을 코드로 구현 하는 것 부터가 어려웠던 문제였다.

손으로 썼을 때는 규칙도 점화식도 알 것 같은데 이걸 코드로 구현하려니 좀 막막했다.
여차저차 코드로 구현은 했는데, 이제는 막상 dp를 통해서 4면체의 개수를 구하는 것이 문제였기 때문에 다른 분이 작성하신 코드를 통해서 깨닳았다.

아직 까지도 dp문제는 힘들기만하다. 조금 더 노력해봐야 하는 분류인 것 같다.

ref.

https://devlibrary00108.tistory.com/565