백준[ 16493 | Python ] 오르막 수

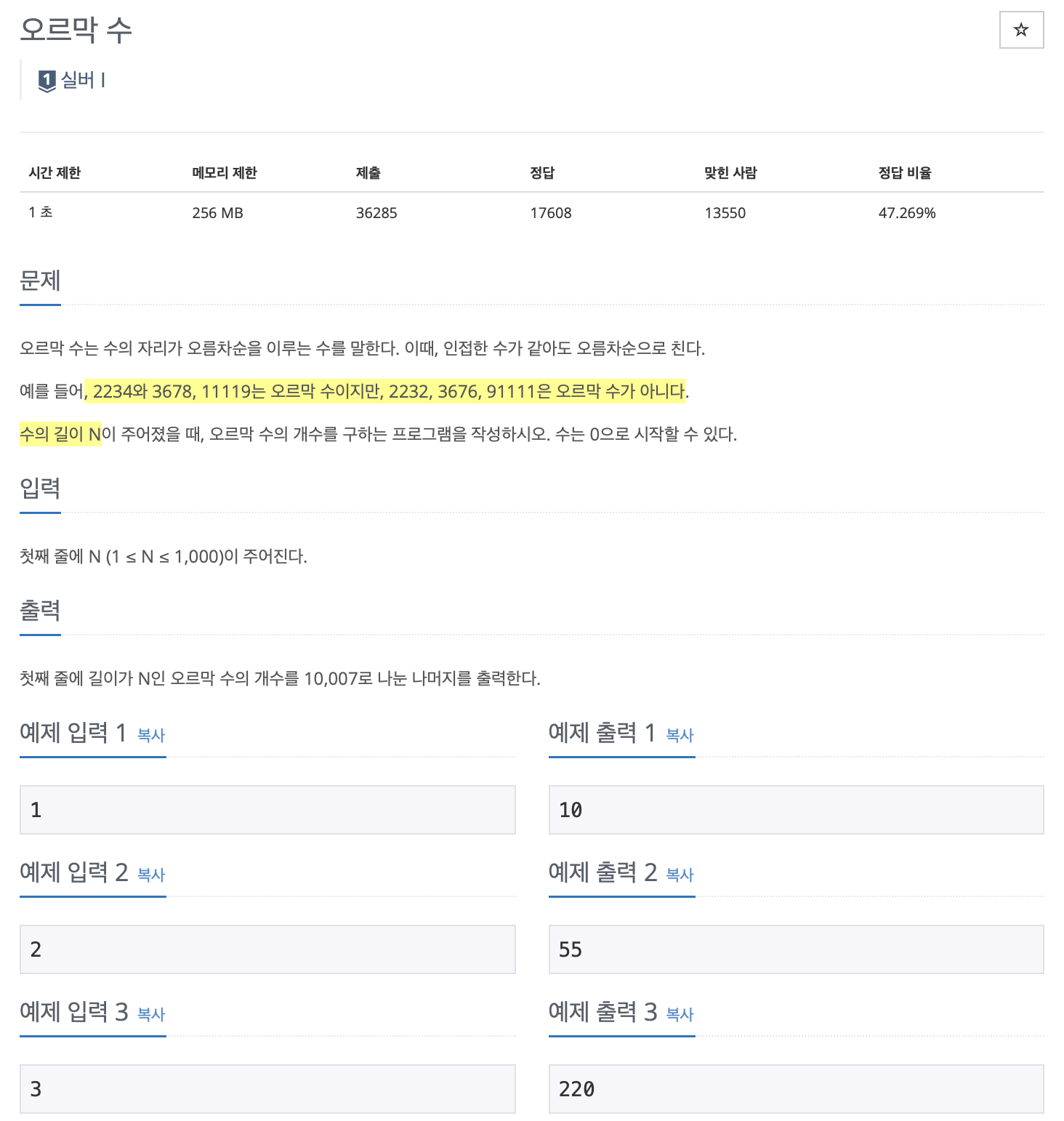
문제

https://www.acmicpc.net/problem/11057

n = int(input())
dp = [[1 for _ in range(10)] for _ in range(n+1)]
for i in range(2, n+1):
    total = sum(dp[i-1])
    for j in range(10):
        dp[i][j] = total
        total-=dp[i-1][j]
print(sum(dp[n])%10007)

생각 & 정리

저번 문제와는 다르게 dp테이블을 2차원 배열로 생성해줘야 하는 문제였다.
n이 1일 때는 각 수 마다 1개의 오르막 수가 존재하는 것으로 여겨 총 10개의 오르막 수가 존재하며
n이 2일 때는 각 수 마다 10개 ~ 1개의 오르막 수가 존재하는 것으로 여긴다.
이를 통해서 n이 3일 때 까지의 결과를 도출하자면 아래의 표와 같다.

n				개수
1	1	1	1	1	1	1	1	1	1	1
2	10	9	8	7	6	5	4	3	2	1
3	55	45	36	28	21	15	10	6	3	1

이 때 주의할 것은 인접한 수가 같으면(11,22와 같은 수) 오르막 수로 간주한다는 것과 0으로 시작하는 수(01, 001 등)를 인정한다는 것이다.

앞서 말했던 조건들을 통해 규칙을 도출 한다면 이전 자리 수에서의 오르막 수의 합으로부터 계속해서 이전에 존재했던 오르막 수의 개수를 빼주면 현재 자리 수와 현재 앞자리 수의 오르막 수를 알아낼 수 있다.